From https://link.springer.com/article/10.1007/JHEP11(2020)007

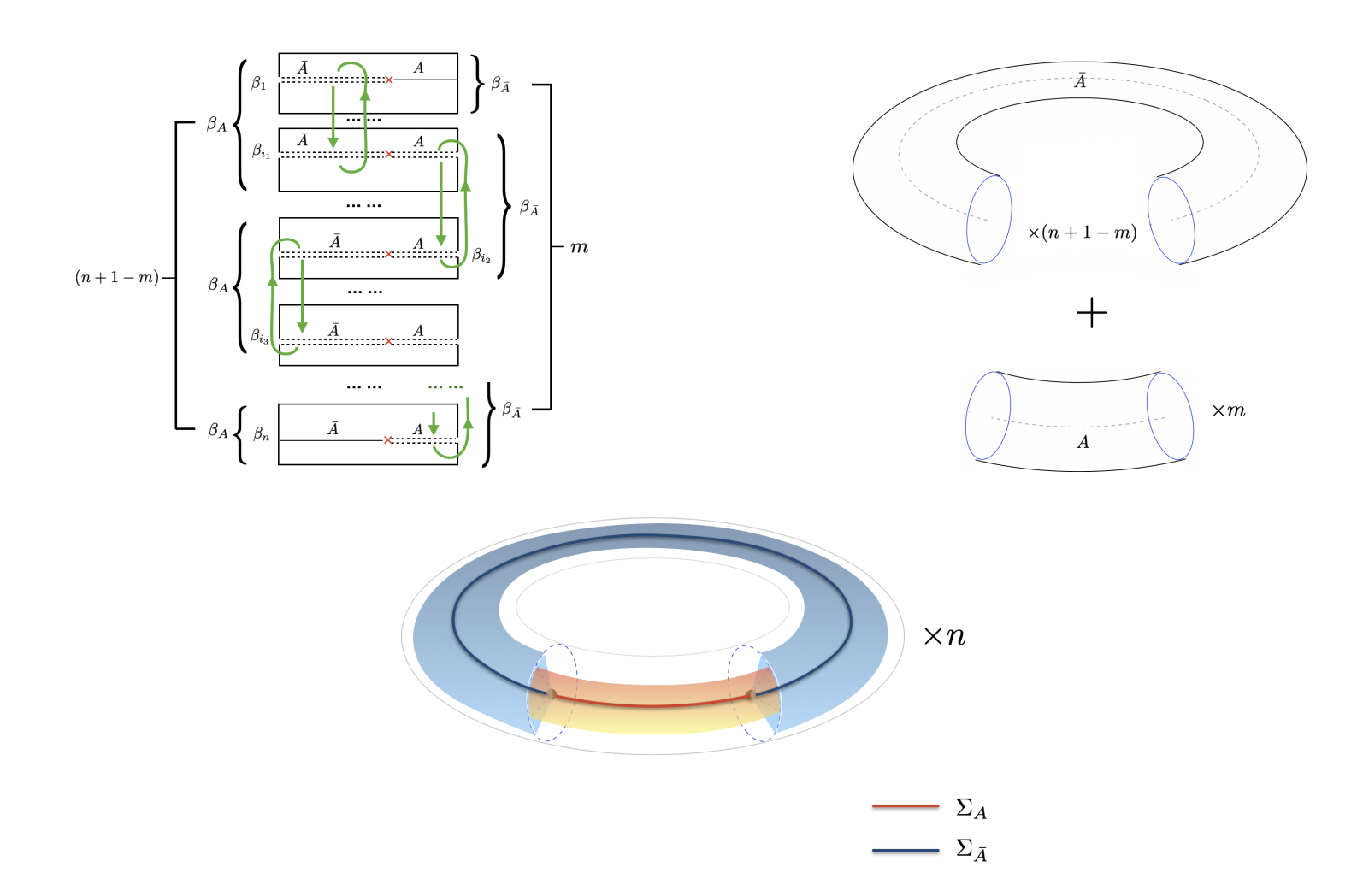
Recent work found an enhanced correction to the entanglement entropy of a subsystem in a chaotic energy eigenstate. The enhanced correction appears near a phase transition in the entanglement entropy that happens when the subsystem size is half of the entire system size. Here we study the appearance of such enhanced corrections holo-graphically. We show explicitly how to find these corrections in the example of chaotic eigenstates by summing over contributions of all bulk saddle point solutions, including those that break the replica symmetry. With the help of an emergent rotational symmetry, the sum over all saddle points is written in terms of an effective action for cosmic branes. The resulting Renyi and entanglement entropies are then naturally organized in a basis of fixed-area states and can be evaluated directly, showing an enhanced correction near holographic entanglement transitions. We comment on several intriguing features of our tractable example and discuss the implications for finding a convincing derivation of the enhanced corrections in other, more general holographic examples.

Authors: Xi Dong and Huajia Wang